앞선 포스팅에서 다중표현이 존재하는 데이터의 예시로 복소수 데이터 모델을 설계해 보았다.
2024.03.06 - [SICP] - 다중표현이 존재하는 데이터 구조 설계(1) - 복소수 모델
그런데 복소수의 사칙연산을 복소수뿐 아니라 실수, 정수, 유리수등의 데이터와의 연산으로 확장하려면 어떻게 해야 할까?
예를 들어 실수 + 복소수 덧셈연산을 정의한다고 해보자. 앞의 방식을 그대로 사용한다면 install 함수 내부에서 연산-형식 테이블에 해당 연산을 정의하면 될 것 같다.
// 실수 연산 패키지
function install_real_package() { ... }
// 복소수 연산 패키지
function install_complex_package() {
...
function add_complex_real(z, x){
return make_from_real_imag(real_part(z) + x, imag_part(z));
}
function tag(z) { return attach_tag("complex", z); }
...
put("add", list("complex", "real"), (z, x) => tag(add_complex_real(z, x)));
put("add", list("real", "complex"), (x, z) => tag(add_complex_real(z, x)));
}
complex 패키지 내부에 정의해 보았다. 이 방식으로도 복소수와 정수의 add 연산에 대해 정상적으로 동작할 것임은 분명하다.
그런데... 뭔가 구린내가 난다.
구린내의 원인
1️⃣ 서로 다른 피연산자 타입의 모든 경우의 수에 대해 비슷한 함수를 반복해서 정의해야 한다.
위에서도 복소수 + 실수, 실수 + 복소수 케이스를 각각 정의했다. 이런 코드를 연산함수 가짓수 x 타입의 순열 가짓수 만큼 작성해야 한다..
2️⃣ 서로 다른 피연산자 타입의 어느 쪽 패키지에 정의할지 고민해야 한다.
나는 위의 함수를 install_real_package, install_complex_package 둘 중에 어느 쪽에 정의할지 고민했는데, 두 연산의 결괏값이 complex이니 "complex" tag를 자연스럽게 붙이기 위해 complex 패키지 내부에 정의했다. 그런데 타입을 추가할 때마다 매번 이런 고민을 해야 한다고?
3️⃣ 어느 쪽 패키지에 정의해야 할지에 대한 아주 명확하고 합리적인 컨벤션을 정했다고 해도, 다른 타입에 의존성 있는 패키지를 만들게 되는 것 자체가 불편하다. complex 패키지 내부에서는 오로지 complex에 대한 연산만 정의하고 싶다.
강제 형변환: 코어션(Coercion)
완전히 연관성이 없는 두 타입 간의 연산을 정의하기 위해서는 번거롭더라도 위에서 제시한 방식을 사용해야만 하는 경우도 있다.
다행히도 실수 - 복소수 타입은 연관성이 있기에 강제 형변환(coercion)을 적용하여 문제를 더 쉽게 풀어내는 게 가능하다.
실수-복소수 연산은 실수를 imag_part(허수부)가 0인 복소수로 바라보아 복소수-복소수 연산으로 처리할 수 있다.
다시 말해, 실수 -> 복소수로 강제 형변환하여 복소수끼리의 연산으로 변환하는 것이다.
function real_to_complex(n) {
return make_complex_from_real_imag(contents(n), 0); // 허수부 0 인 복소수로 변환
}실수 -> 복소수 형변환 함수는 이처럼 간단하게 정의할 수 있다.
그리고 이런 형변환 연산들도 data-directed programming방식을 적용하여 앞에서 연산-형식 테이블을 관리했던 것과 마찬가지로 coercion 테이블을 만들어서 관리할 수 있다.
put_coercion("real", "complex", real_to_complex); 이제 일반적 함수를 적용할 때 형변환을 사용할 수 있도록 apply_generic 내부 로직을 다음과 같이 수정한다.
function apply_generic(op, args){
const type_tags = map(type_tag, args);
const fun = get(op, type_tags); // 연산-형식 테이블에서 적용할 함수 추출
if (fun){
return apply(fun, map(contents, args));
}
// coercion
if (length(args) === 2){
const type1 = head(type_tags);
const type2 = head(tail(type_tags));
const a1 = head(args);
const a2 = head(tail(args));
const t1_to_t2 = get_coercion(type1, type2);
const t2_to_t1 = get_coercion(type2, type1);
return t1_to_t2
? apply_generic(op, list(t1_to_t2(a1), a2))
: t2_to_t1
? apply_generic(op, list(a1, t2_to_t1(a2)))
: error(list(op, type_tags), "no method for these types"); // 형변환 불가
}
return error(list(op, type_tags), "no method for these types");
}
정리
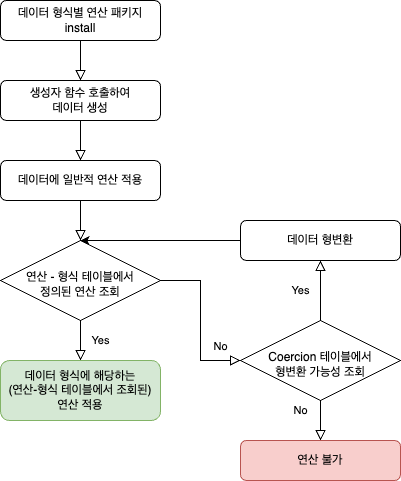
지금까지의 내용을 종합하면, 다중표현 데이터에 일반적 연산을 적용하는 과정을 다음과 같은 플로우차트로 나타낼 수 있다.
타입의 계층 구조
위에서 다른 타입 간의 연산을 위해 강제 형변환을 활용할 수 있었던 것은 두 타입 간 자연스러운 관계 정의가 가능했기 때문이다.
실수를 특수한 종류의 복소수로 간주할 수 있었는데, 이런 경우 타입 간 계층 구조를 가진다고 할 수 있다. 복소수는 실수의 상위 타입이 된다.
이렇게 여러 유형 간의 관계가 특정한 계층구조를 가지게 되면 다중 타입들의 연산을 정의하는 문제를 크게 단순화시킬 수 있다.
예를 들어, 정수, 유리수, 실수, 복소수를 처리하는 일반 산술 시스템을 구축한다고 가정해 보자.
각 타입은 최대 하나의 상위 타입과 최대 하나의 하위 타입을 가지며 이러한 계층구조를 Tower라고 한다.
타입들이 Tower 계층 구조를 이루면 다음과 같은 이점들이 있다.
1️⃣ 타입 간의 변환 함수는 바로 상위에 위치한 타입으로 변환하는 함수만 제공하면 된다. 즉, 모든 타입변환 케이스에 대해 일일이 정의할 필요가 없다.
정수 -> 유리수, 유리수 -> 실수, 실수 -> 복소수 변환 함수 세 가지만 정의해 두면 연쇄적으로 형변환하는 전략을 사용하여 그 외의 형변환 케이스를 모두 처리할 수 있다.
2️⃣ 모든 타입이 상위 타입에 정의된 모든 작업을 상속한다는 개념을 쉽게 구현할 수 있다.
상위타입에 정의된 연산은 하위타입에서 따로 구현하지 않아도 형변환을 통해 상위타입 연산을 자연스럽게 이용할 수 있다.
3️⃣ 데이터 객체를 가장 단순한 표현으로 낮추는 간단한 방법을 제공할 수 있다.
상위표현 간의 연산결과가 하위표현으로 더 단순하게 나타낼 수 있는 상황이 발생할 수 있다. (ex. (1+i) + (2-i) = 3은 복소수의 연산이지만 정수로 답을 구하는 게 좋을 것이다.)
이를 위해서는 상위타입 -> 하위타입 변환 함수들을 corecion 테이블에 정의해 두고, 1️⃣ 과 마찬가지로 연쇄적 하강 작업을 구현하면 된다.
'프로그래밍 > SICP' 카테고리의 다른 글
| 동시성 제어 - by 직렬화(serialization) (0) | 2024.03.23 |
|---|---|
| 다중표현이 존재하는 데이터 구조 설계(1) - 복소수 모델 (0) | 2024.03.06 |
| 허프먼 부호화 트리 구현과 복호화 (0) | 2024.02.28 |
| 닫힘 성질을 충족하는 데이터 구조 설계(2) - 예제: 그림언어 (1) | 2024.02.27 |
| 닫힘 성질을 충족하는 데이터 구조 설계(1) (0) | 2024.02.24 |




